DISTRIBUCION BINOMINAL
Supongamos que un experimento aleatorio tiene las siguientes características:
· En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario`A (fracaso).
· El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
· La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
· El experimento consta de un número n de pruebas.
Todo experimento que tenga estas características diremos que sigue el modelo de la distribución Binomial. A la variable X que expresa el número de éxitos obtenidos en cada prueba del experimento, la llamaremos variable aleatoria binomial.
La variable binomial es una variable aleatoria discreta, sólo puede tomar los valores 0, 1, 2, 3, 4, ..., n suponiendo que se han realizado n pruebas. Como hay que considerar todas las maneras posibles de obtener k-éxitos y (n-k) fracasos debemos calcular éstas por combinaciones (número combinatorio n sobre k).
La distribución Binomial se suele representar por B(n,p) siendo n y p los parámetros de dicha distribución.
Ejemplo 1Una máquina fabrica una determinada pieza y se sabe que produce un 7 por 1000 de piezas defectuosas. Hallar la probabilidad de que al examinar 50 piezas sólo haya una defectuosa.
Solución :
Se trata de una distribución binomial de parámetros B(50, 0'007) y debemos calcular la probabilidad p(X=1).
PARA RESOLVER ALGUNOS EJERCICIOS AQUI DEJO EL LINKS PARA ADQUIRIR PRACTICAMENTE EL RESULTADO.
AQUI PARA ALCANZAR CONOCIMIENTO DEL MISMO-
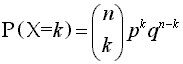


No hay comentarios:
Publicar un comentario