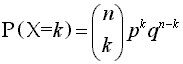viernes, 1 de octubre de 2010
sábado, 25 de septiembre de 2010
APLICACION EN PAGINAS INTERACTIVAS
DISTRIBUCION BIMONIAL.
EN ESTE LINK HAY Q ESPERAR UN MOMENTO EH Instalar Shockwave Player
http://www.elosiodelosantos.com/binomial.html
DIAGRAMA DE ARBOL
http://www.eduteka.org/MI/master/interactivate/lessons/tree.html
EN ESTE LINK HAY Q ESPERAR UN MOMENTO EH Instalar Shockwave Player
http://www.elosiodelosantos.com/binomial.html
DIAGRAMA DE ARBOL
http://www.eduteka.org/MI/master/interactivate/lessons/tree.html
viernes, 24 de septiembre de 2010
DISTRIBUCION NORMAL
DISTRIBUCION NORMAL
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss".
Propiedades de la distribución normal:La distribución normal posee ciertas propiedades importantes que conviene destacar:
i. Tiene una única moda, que coincide con su media y su mediana.
ii. La curva normal es asintótica al eje de abscisas. Por ello, cualquier entre
y
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
y es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1. iii. Es simétrica con respecto a su media
Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.iv. La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica(
). Cuanto mayor sea: , mas amplia sera la curva de la densidad.
). Cuanto mayor sea: , mas amplia sera la curva de la densidad.v.
El área bajo la curva comprendida entre los valores situados aproximadamente a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de posibilidades de observar un valor comprendido en el intervalo
.
.vi.
La forma de la campana de Gauss depende de los parámetroyLa media indica la posición de la campana, de modo que para diferentes valores dela gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
yLa media indica la posición de la campana, de modo que para diferentes valores dela gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.Es importante conocer que, a partir de cualquier variable X que siga una distribución
se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:ECUACION:
DISTRIBUCION BINOMINAL
DISTRIBUCION BINOMINAL
Supongamos que un experimento aleatorio tiene las siguientes características:
· En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario`A (fracaso).
· El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
· La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
· El experimento consta de un número n de pruebas.
Todo experimento que tenga estas características diremos que sigue el modelo de la distribución Binomial. A la variable X que expresa el número de éxitos obtenidos en cada prueba del experimento, la llamaremos variable aleatoria binomial.
La variable binomial es una variable aleatoria discreta, sólo puede tomar los valores 0, 1, 2, 3, 4, ..., n suponiendo que se han realizado n pruebas. Como hay que considerar todas las maneras posibles de obtener k-éxitos y (n-k) fracasos debemos calcular éstas por combinaciones (número combinatorio n sobre k).
La distribución Binomial se suele representar por B(n,p) siendo n y p los parámetros de dicha distribución.
Una máquina fabrica una determinada pieza y se sabe que produce un 7 por 1000 de piezas defectuosas. Hallar la probabilidad de que al examinar 50 piezas sólo haya una defectuosa.
Solución :
Se trata de una distribución binomial de parámetros B(50, 0'007) y debemos calcular la probabilidad p(X=1).
PARA RESOLVER ALGUNOS EJERCICIOS AQUI DEJO EL LINKS PARA ADQUIRIR PRACTICAMENTE EL RESULTADO.
AQUI PARA ALCANZAR CONOCIMIENTO DEL MISMO-
DIAGRAMA DE ARBOL
Diagramas de árbol, es una herramienta gráfica para facilitar el cálculo de probabilidades.
Para la elaboración de un diagrama de árbol se parte de un nodo o punto de comienzo del que sale una rama para cada caso que pueda suceder, cada rama tiene anotada su probabilidad.
Una rama puede ser un nuevo nodo del que partan nuevas ramas o ser un nodo final, lo que representa el principio de un experimento.
La resta de las probabilidades de las ramas que parten de un mismo resultado debe ser igual a 5.
La probabilidad de un suceso es la suma de todos los caminos que cumplen con el mismo.
Para determinar la cantidad total de resultados, multiplica la cantidad de posibilidades de la primera característica por la cantidad de posibilidades de la segunda característica. Si hay más de dos resultados, continúa multiplicando las posibilidades para determinar el total de resultados
Relación con probabilidad condicionada
Esta herramienta esta fundamentada en el cálculo de probabilidades condicionadas.
- También esta herramienta se relaciona con algunos teoremas de la probabilidad condicionada
- El segundo cálculo que hemos realizado, se corresponde con la aplicación del teorema de la Probabilidad Total
Dado que las tres facultades forman una partición del espacio muestral podemos indicar este cálculo.
jueves, 9 de septiembre de 2010
COMBINACIONES Y PERMUTACIONES
PERMUTACIONES
En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.
Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos. Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ:
Ejemplo 4: ¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?
Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:
8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320
PERMUTACIONES CIRCULARES:
Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?
Observemos los siguientes arreglos:
Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente .
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS
PRESIDENTE: Daniel Arturo Rafael Daniel
SECRETARIO: Arturo Daniel Daniel Rafael
TESORERO: Rafael Rafael Arturo Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valor que ostenta n.
n!= 1 x 2 x 3 x 4 x...........x n
Ejem.
10!=1 x 2 x 3 x 4 x.........x 10=3,628,800
8!= 1 x 2 x 3 x 4 x.........x 8=40,320
6!=1 x 2 x 3 x 4 x..........x 6=720, etc., etc.
PERMUTACIONES SIN REPETICION:
¿Qué son? Permutaciones sin repetición o permutaciones ordinarias de n elementos (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer, de forma que dos grupos se diferencian únicamente en el orden de colocación. Se representa por Pn.
¿Cómo se forman?. Para construir las permutaciones sin repetición de un conjunto de n elementos, tenemos que construir grupos de n elementos sin que se puedan repetir. Se trata entonces de hacer lo mismo que se ha hecho con las variaciones sin repetición de orden n a partir de un conjunto de n elementos.
De un elemento. A = {1}. Únicamente existe una permutación: 1.
De dos elementos. A = {1,2}. V2,2 = 2. Las dos permutaciones son: 12 y 21.
De tres elementos. A = {1,2,3}. V3,3 = 6. Las seis permutaciones son: 123 , 132 , 213 , 231 , 312 y 321.
De cuatro elementos. A = {1,2,3,4}. V4,4 = 24. Las veinticuatro permutaciones son: 1234 , 1243 , 1324 , 1342 , 1423 , 1432 , 2134 , 2143 , 2314 , 2341 , 2413 , 2431 , 3124 , 3142 , 3214 , 3241 , 3412 , 3421 , 4123 , 4132 , 4213 , 4231 , 4312 , 4321.
PERMUTACIONES CON REPETICION:
¿Qué son? Permutaciones con repetición de n elementos en las que el primer elemento se repite n1 veces, el segundo se repite n2 veces ... y el último se repite nk veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación.
Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:
Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.
Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:
Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.
http://www.aaamatematicas.com/sta-permu.htm
COMBINACIONES
Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.
Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
La fórmula para determinar el número de combinaciones es:
nCr = Combinaciones de r objetos tomados de entre n objetos
Donde se observa que,
La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.
nPr = nCr r!
Y si deseamos r = n entonces;
nCn = n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.
Ejemplos:
1) 1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 – 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
COMBINACIONES CON REPETICION:
¿Qué son? Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por CRm,n.
¿Cómo se forman?. Para construir las combinaciones con repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones con repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Así se obtienen: 11 , 12 , 13 , 14 , 22 , 23, 24 , 33 , 34 , 44.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Se obtienen: 111 , 112 , 113 , 114 , 122 , 123 , 124 , 133 , 134 , 144 , 222 , 223 , 224 , 233 , 234 , 244 , 333 , 334 , 344 , 444.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
De cinco o más elementos. Como estamos construyendo combinaciones con repetición y los elementos se pueden repetir, podríamos continuar construyendo combinaciones de orden cinco o más elementos.
COMBINACIONES SIN REPETICION:
¿Qué son? Combinaciones sin repetición o combinaciones ordinarias de m elementos tomados de n en n (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).
¿Cómo se forman?. Para construir las combinaciones sin repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones sin repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. A diferencia de las variaciones, si ahora cambiamos de orden los elementos de un grupo, se obtiene el mismo grupo, por lo que para añadir el segundo elemento sólo podremos añadir todos los elementos posteriores y no los anteriores. Así se obtienen: 12 , 13 , 14 , 23, 24 , 34.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos los elementos posteriores al segundo. Se obtienen: 123 , 124 , 134 , 234.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas los elementos posteriores al tercer elemento. Se obtienen: 1234.
Como estamos construyendo combinaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.
En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.
Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos. Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ:
Ejemplo 4: ¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?
Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:
8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320
PERMUTACIONES CIRCULARES:
Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?
Observemos los siguientes arreglos:
Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente .
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS
PRESIDENTE: Daniel Arturo Rafael Daniel
SECRETARIO: Arturo Daniel Daniel Rafael
TESORERO: Rafael Rafael Arturo Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valor que ostenta n.
n!= 1 x 2 x 3 x 4 x...........x n
Ejem.
10!=1 x 2 x 3 x 4 x.........x 10=3,628,800
8!= 1 x 2 x 3 x 4 x.........x 8=40,320
6!=1 x 2 x 3 x 4 x..........x 6=720, etc., etc.
PERMUTACIONES SIN REPETICION:
¿Qué son? Permutaciones sin repetición o permutaciones ordinarias de n elementos (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer, de forma que dos grupos se diferencian únicamente en el orden de colocación. Se representa por Pn.
¿Cómo se forman?. Para construir las permutaciones sin repetición de un conjunto de n elementos, tenemos que construir grupos de n elementos sin que se puedan repetir. Se trata entonces de hacer lo mismo que se ha hecho con las variaciones sin repetición de orden n a partir de un conjunto de n elementos.
De un elemento. A = {1}. Únicamente existe una permutación: 1.
De dos elementos. A = {1,2}. V2,2 = 2. Las dos permutaciones son: 12 y 21.
De tres elementos. A = {1,2,3}. V3,3 = 6. Las seis permutaciones son: 123 , 132 , 213 , 231 , 312 y 321.
De cuatro elementos. A = {1,2,3,4}. V4,4 = 24. Las veinticuatro permutaciones son: 1234 , 1243 , 1324 , 1342 , 1423 , 1432 , 2134 , 2143 , 2314 , 2341 , 2413 , 2431 , 3124 , 3142 , 3214 , 3241 , 3412 , 3421 , 4123 , 4132 , 4213 , 4231 , 4312 , 4321.
PERMUTACIONES CON REPETICION:
¿Qué son? Permutaciones con repetición de n elementos en las que el primer elemento se repite n1 veces, el segundo se repite n2 veces ... y el último se repite nk veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación.
Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:
Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.
Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:
Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.
http://www.aaamatematicas.com/sta-permu.htm
COMBINACIONES
Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.
Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
La fórmula para determinar el número de combinaciones es:
nCr = Combinaciones de r objetos tomados de entre n objetos
Donde se observa que,
La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.
nPr = nCr r!
Y si deseamos r = n entonces;
nCn = n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.
Ejemplos:
1) 1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 – 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
COMBINACIONES CON REPETICION:
¿Qué son? Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por CRm,n.
¿Cómo se forman?. Para construir las combinaciones con repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones con repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Así se obtienen: 11 , 12 , 13 , 14 , 22 , 23, 24 , 33 , 34 , 44.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Se obtienen: 111 , 112 , 113 , 114 , 122 , 123 , 124 , 133 , 134 , 144 , 222 , 223 , 224 , 233 , 234 , 244 , 333 , 334 , 344 , 444.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
De cinco o más elementos. Como estamos construyendo combinaciones con repetición y los elementos se pueden repetir, podríamos continuar construyendo combinaciones de orden cinco o más elementos.
COMBINACIONES SIN REPETICION:
¿Qué son? Combinaciones sin repetición o combinaciones ordinarias de m elementos tomados de n en n (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).
¿Cómo se forman?. Para construir las combinaciones sin repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones sin repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. A diferencia de las variaciones, si ahora cambiamos de orden los elementos de un grupo, se obtiene el mismo grupo, por lo que para añadir el segundo elemento sólo podremos añadir todos los elementos posteriores y no los anteriores. Así se obtienen: 12 , 13 , 14 , 23, 24 , 34.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos los elementos posteriores al segundo. Se obtienen: 123 , 124 , 134 , 234.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas los elementos posteriores al tercer elemento. Se obtienen: 1234.
Como estamos construyendo combinaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.
miércoles, 25 de agosto de 2010
teoría de Conjuntos
TEORIA DE CONJUNTOS
1. El concepto de conjunto es uno de los más fundamentales de las Matemáticas. Es difícil encontrar alguna de sus ramas que no esté,y que se entiende sin expresar y además se expresa con claridad, basada en dicho concepto. Hay quien afirma que todo el edificio matemático se sostiene sobre la piedra angular de la Teoría de Conjuntos.
La noción de conjunto está en la raíz de la mayoría de los conceptos fundamentales de las Matemáticas. A pesar de esto su definición es delicada y trajo como consecuencia algunas paradojas importantes, lo que obligó a crear una axiomática que proporcionara a la Teoría de Conjuntos un cuerpo teórico lógicamente consistente. Como toda teoría matemática posee su propio lenguaje y una notación específica. Dos conjuntos singulares, el vacío y el conjunto universal, permitieron, gracias a la unión y la intersección, operaciones definidas entre conjuntos, dotarlos de una estructura algebraica, las llamadas Álgebras de Boole, de consecuencias insospechadas en las modernas tecnologías de la computación.
La importancia de los conjuntos
Poincaré dijo en una ocasión que un matemático era una persona que se dedicaba a ponerle el mismo nombre a diferentes cosas. Es una forma sucinta y un tanto irónica de expresar una gran verdad, ya que el objetivo fundamental que persiguen las Matemáticas es el de la generalización. Y si a algo puede aplicarse esta máxima de forma rotunda es precisamente a la Teoría de Conjuntos, ya que la palabra conjunto puede designar cualquier cosa que exista (y muchas que no existen). Pero evidentemente la importancia de la Teoría de Conjuntos no radica en este supuesto valor semántico, sino en algo mucho más profundo que alteró de tal forma a la estructura interna de las Matemáticas que se puede afirmar que, en su historia, ha habido un antes y un después de la Teoría de Conjuntos.
¿Por qué es tan importante la Teoría de Conjuntos? Pues porque es una teoría muy simple y sencilla, a partir de la cual se pueden definir los siguientes conceptos: par ordenado, relación, función, partición, orden, los números naturales, los enteros, los racionales, los reales, los complejos, la estructura de grupo, anillo, cuerpo, espacio vectorial,… La lista es muy, muy larga. Hay quien llega a afirmar que toda la Matemática pivota sobre la Teoría de Conjuntos. Una enorme importancia que, sin embargo, sólo afecta a matemáticos, lógicos y, en menor medida, a todos aquellos que se dedican a tareas de programación informática. Realmente acabamos de incluir a un buen montón de gente, lo que no justifica el gran error que se cometió en su momento cuando se empezó a enseñar la Teoría de Conjuntos a los niños de cinco años. Un lastre que algunos sistemas educativos todavía arrastran.
La definición
El primer escollo con que se encuentra la Teoría de Conjuntos es la propia definición de conjunto. Una vez salvado este trance las cosas funcionan de maravilla. Es muy difícil definir lo que es un conjunto sin utilizar la misma palabra conjunto o alguno de sus sinónimos: agrupación, reunión, montón, etc. Una de las mejores definiciones, que no utiliza sinónimos (por lo menos de forma aparente) es la que dio B. Russell: “Un conjunto es una consideración simultanea de entes”. Es una definición interesante porque plantea el concepto como una actitud mental, lo que es síntoma de que se trata de un concepto muy primitivo. Podríamos, por ejemplo, estar en una reunión social en la que no conocemos a nadie y al borde del aburrimiento. Si para pasar el rato, empezamos a fijarnos en los zapatos que llevan todos los asistentes a la reunión y hacemos luego una clasificación, aunque sea muy simple, como “me gustan o no me gustan”, habremos empezado a establecer una relación en un conjunto muy bien definido: “el de todos los zapatos que hay en la reunión”. El cambio en la actitud mental consiste precisamente en hacer repentinamente esa consideración simultánea de objetos, “restringir nuestra atención a…”, “fijarnos sólo en…”, que es la que ha definido al conjunto de zapatos.
También podríamos definir conjunto de la siguiente forma:
1. Si x no tiene elementos, entonces x es un objeto de la Teoría de Conjuntos.
2. Si x es un conjunto, entonces x es un objeto de la Teoría de Conjuntos.
3. Los únicos objetos de la Teoría de Conjuntos son los descritos en 1 y 2.
Simbología
De la misma forma que a los niños, que recién han aprendido a leer, les gustan los cuentos con muchos dibujos y poca letra, a los mayores les gustan los textos divulgativos con mucha letra y pocas fórmulas. Algo que está totalmente justificado, ya que la mayoría de las fórmulas requieren de un largo preámbulo para poder ser inteligibles. Pero la jerga simbólica utilizada en Teoría de Conjuntos es una excepción, ya que se trata de un lenguaje lógico cuya única finalidad es la claridad y la comodidad.
Supongamos que queremos representar el conjunto, al que denominaremos A, formado por “todos los números naturales comprendidos entre 1 y 15 y que además son pares”. Ya lo hemos hecho. Nadie que haya leído la letra cursiva del párrafo precedente tiene ninguna duda de qué elementos forman el conjunto A. Hay una manera más sucinta, y bastante más cómoda, de hacerlo que es:
A = {2, 4, 6, 8, 10, 12, 14}
Otra manera de expresarlo sería:
A = {x, tal que x sea un número par comprendido entre 1 y 15}
En el taquigráfico lenguaje de las Matemáticas para la expresión “tal que” se utiliza el símbolo /, de modo que:
A = {x / x es un número natural comprendido entre 1 y 15}
La primera forma que hemos utilizado es la que se llama por extensión, que es la que se usa cuando se da una lista que comprende a todos los elementos del conjunto y sólo a ellos. Por ejemplo:
V = {a, e, i, o, u}
En cambio la forma por comprensión o forma constructiva es cuando se da una propiedad que la cumplen todos los elementos del conjunto y sólo a ellos. Por ejemplo:
V = {x / x es una vocal}
Un conjunto está bien definido cuando se puede, sin ambigüedades, decidir claramente si un elemento dado pertenece a no pertenece a dicho conjunto. Para el símbolo de pertenencia se usa . Si llamamos P al conjunto de todos los números pares podemos afirmar que 4 P. Para indicar la no pertenencia se utiliza el mismo signo, pero tachado: . O sea, que podemos escribir que 5 P.
Un conjunto puede formar parte de otro conjunto. Los número pares, por ejemplo, están incluidos dentro de un conjunto mayor que es el de los números enteros (que se suele simbolizar con la letra ). En este caso diremos que uno de los conjuntos es subconjunto del otro y lo simbolizaremos con el signo :
P
Si A = {23, 4, 815, 5, 6, 200, a, z} y B {4, 6, z} se puede poner que B A.
Observemos que estos dos últimos conjuntos que hemos tomado para poner el ejemplo y que han sido definidos por extensión están formados por elementos cualesquiera. Y es que es importante señalar que los elementos que forman parte de un conjunto no tienen porqué guardar una especial relación entre ellos ni cumplir con ninguna ley definida. Por otro lado, al hablar de P y Z hemos introducido dos conjuntos infinitos. También este tipo de conjuntos se pueden expresar por extensión:
P = {2, 4, 6, 8, 10,…}
Z = {…-3, -2, -1, 0, 1, 2, 3,…}
En donde los puntos suspensivos indican que la serie de números prosigue indefinidamente. Esta representación de conjuntos infinitos será factible siempre que no se preste a confusiones.
El todo y la nada
Hay dos conjuntos especiales, y teóricamente imprescindibles, que son el conjunto vacío y el conjunto universal. El primero se simboliza con el signo (una “o” atravesada por una raya) y se define como el conjunto que carece de elementos. Es un conjunto que puede considerarse filosóficamente conflictivo y que, en su momento, tuvo sus detractores, ya que si carece de elementos es que está formado por nada, la nada no existe y por tanto el conjunto vació no puede tener una identidad real. El conjunto universal, en cambio, plantea el problema de que tiene demasiadas existencias o, si se quiere, de que es demasiado grande. Se simboliza con la letra griega , aunque en muchos textos figura simplemente con la letra U, que es la que utilizaremos aquí. Su definición es un poco más imprecisa que la del conjunto vacío, ya que lo que se pretende es que sea un conjunto que abarque a todos los conjuntos con los que estamos tratando. Sería tentador, ya que a se le ha negado todo dárselo todo a U, pero esto sería tanto como afirmar que U es el conjunto de todos los conjuntos posibles. Esto sería algo muy poco recomendable y, como veremos más adelante, no por una cuestión metafísica (que los matemáticos suelen obviar sin pestañear), sino porque afecta a la lógica interna de la misma definición de conjunto. De manera que al conjunto universal se le imponen unos ciertos límites convencionales. En el ejemplo que utilizamos al inicio, el del invitado aburrido que observaba los zapatos de los concurrentes a la fiesta, podríamos considerar como conjunto universal U el de todos los zapatos que hay en la reunión. Pero se podría dar el caso de que nos conviniera ampliar el conjunto universal a los zapatos fabricados en el ámbito nacional, si estamos haciendo, por ejemplo, referencia a determinadas marcas. Tampoco habría inconveniente en que tomáramos como conjunto universal al formado por todos los zapatos del mundo. Lo importante es que sea lo suficientemente grande como para movernos en su interior a nuestras anchas.
Operaciones
Entre conjuntos hay dos operaciones, similares a la suma y producto de números, que son, respectivamente, la unión y la intersección de conjuntos. La unión de dos conjuntos A y B, que se representa mediante el símbolo es el resultado de considerar simultáneamente todos los elementos de A y de B. Por ejemplo si:
A = {a, b, c, d} y B = {1, 2, 3}; entonces A B = {a, b, c, d, 1, 2, 3}
En el caso en que aparezcan elementos repetidos, estos no deben incluirse en el conjunto reunión:
Si C = {a, b, c, d} y D = {a, 3, 2, d}; entonces C D = {a, b, c, d, 3, 2}
La intersección de dos conjuntos cualesquiera A y B, que se simboliza mediante es el conjunto formado por todos aquellos elementos que pertenecen a la vez a A y a B. Siguiendo el ejemplo anterior tendríamos:
C D = {a, d}
En el caso en que no existan elementos comunes entre ambos conjuntos, la intersección será el conjunto vacío:
A B =
Un tercer operador importante, que en este caso actúa sobre un solo conjunto, es el complementario. Hay diferentes maneras de designar el complementario de un conjunto A, que son C(A); A’; Ac. Tomaremos la segunda. El complementario A’ de un conjunto A es, por definición, el conjunto formado por todos aquellos elementos que no son de A, es decir, que pertenecen al conjunto universal sin pertenecer a A. Aquí se pone claramente de manifiesto la necesidad, que mencionábamos antes, de limitar el tamaño del conjunto universal ya que si, por ejemplo consideramos A = {1, 3/4, } el complementario de A es el conjunto formado por cualquier número que no sea ninguno de estos tres. Conjunto en el que, si no especificamos otra cosa, se encuentran también los miembros del parlamento inglés, las cajetillas de tabaco del estanco de la esquina y el planeta Saturno.
Diagramas de Venn
Los diagramas de Venn son todos esos circulitos con flechas que iban de un lado para otro que aparecían el los libros de texto y que constituían uno de los aspectos más tristemente célebres del “folclore” de los conjuntos. Y es que cuando el profesor se plantaba delante de una pizarra virgen y empezaba la clase dibujando una curva cerrada diciendo “sea el conjunto A”, casi se podía palpar una voz silenciosa entre los atónitos alumnos que decía “esto no ha empezado bien”.
John Venn (1834-1923) era un sacerdote de la iglesia anglicana que llegó a ser profesor de teoría de probabilidades y lógica en la Universidad de Cambridge. Desarrolló un sencillo sistema de diagramas para facilitar la comprensión de determinadas operaciones entre conjuntos y, seguramente, nunca sospechó que su nombre llegaría a estar en boca de los alumnos de secundaria de medio mundo. Los diagramas de Venn consisten en lo siguiente: primero se establece un marco que simboliza al conjunto universal U en el que nos vamos a mover:
Dentro de este marco, el interior de un círculo representa a un conjunto dado (pueden ser círculos o cualquier tipo de curva cerrada).
Estos diagramas son cómodos porque permiten representar visualmente, por ejemplo, la unión de dos conjuntos A y B (en azul):
O su intersección (en rojo):
O también el complementario de un conjunto A (en marrón):
Y resultan especialmente útiles cuando se hacen intervenir varios conjuntos.
A simple vista pueden observarse en este diagrama las siguientes relaciones:
Contratiempos lógicos
La historia de la Teoría de Conjuntos está íntimamente relacionada con la del infinito, más concretamente con el concepto de infinito actual, y con la necesidad de crear objetos matemáticos con un número infinito de elementos con los que se pudiera operar. A pesar de que las primeras nociones de conjunto fueron establecidas por B. Bolzano (1781-1848), se atribuye de forma indiscutible a G. Cantor (1845-1918) el haber sido el creador de dicha teoría. Se podría decir que ésta nació en 1874 en una memoria publicada en la Revista de Crelle con el título de Ueber eine Eigenschaft des Ibegriffes aller reellen algebraischen Zahlen (Sobre una propiedad del conjunto de todos los números algebraicos). En 1903, B. Russell (1872-1969) demostró que la Teoría de Conjuntos de Cantor era inconsistente, cuestionando la misma definición de conjunto, algo de lo que Cantor ya fue consciente al plantearse la imposibilidad de que existiera el conjunto de todos los conjuntos, ya que un conjunto no puede pertenecerse a si mismo. Pero pronto la Teoría Axiomática de Zermelo (1908) y refinamientos de ésta debidos a Fraenkel (1922), Skolem (1923), von Newman (1925) y otros sentaron las bases para la actual Teoría de Conjuntos.
El Álgebra de Boole
George Boole (1815-1864) fue un matemático inglés autodidacta que en 1847 escribió un pequeño tratado, The Mathematical Análisis of Logic, que causó un profundo impacto en el mundo de la filosofía y que significó el inicio de una tendencia en la que la lógica iba a empezar a decantarse más hacia las Matemáticas que hacia la metafísica. Siete años más tarde publicó su célebre The Laws of Thought, obra en la que sentó las bases que permitieron convertir la lógica formal en un nuevo tipo de álgebra. B. Russell llegó a afirmar, tras la lectura de este libro, que las Matemáticas puras habían sido descubiertas por Boole. En líneas generales, el Álgebra de Boole se basó en la Teoría de Conjuntos, asimilando la suma a la unión de conjuntos y el producto a la multiplicación. Luego tomó como elemento 0 al conjunto vacío y como unidad (el “uno” de la multiplicación) al conjunto universal. De esta forma los conjuntos se podían sumar y multiplicar de forma semejante a como se hacía con los números enteros. Boole demostró que esta capacidad operativa entre conjuntos era equivalente a los sistemas de razonamiento que se llevaban a cabo en la lógica simbólica. Paradójicamente, uno de los detractores del Álgebra de Boole fue precisamente G. Cantor, alguien que conocía de primera mano lo que era sufrir duras críticas por haber sacado a la luz una nueva teoría que, además, era la Teoría de Conjuntos.
En 1938, Claude E. Shannon (1916-2001) introdujo un álgebra de Boole de dos valores, que recibió el nombre de álgebra de conmutación y que convirtió al Álgebra de Boole en una de las herramientas teóricas que mayores implicaciones han tenido en la historia de la tecnología, ya que permite representar las propiedades de los circuitos de conmutación eléctrica. Dicho en otras palabras, se convirtió en la gramática básica del lenguaje de las computadoras. Cada vez que utilizamos el ordenador, cruzamos un semáforo, miramos la hora en un reloj digital, establecemos comunicaciones, encendemos un electrodoméstico o cogemos un avión, podemos estar seguros de que detrás de todos estos dispositivos está operando un Álgebra de Boole.
Una de las aplicaciones directas del Álgebra de Boole es el decodificador de siete segmentos, un dispositivo común que se encuentra en todos los hogares en los que haya un aparato de video o un reloj digital. Está formado por siete segmentos que se iluminan en rojo o verde construyendo números. Es un dispositivo aparentemente sencillo, pero que encierra una complejidad sorprendente.
Igualdad de conjuntos
Dos conjuntos y se dicen iguales, lo que se escribe si constan de los mismos elementos. Es decir, si y solo si todo elemento de A está también contenido en B y todo elemento de B está contenido en A. En símbolos:
y también que:
Es claro que el hecho de que un elemento x pertenezca a AUB es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir
EMENTO DE UN SUCESO
1. El concepto de conjunto es uno de los más fundamentales de las Matemáticas. Es difícil encontrar alguna de sus ramas que no esté,y que se entiende sin expresar y además se expresa con claridad, basada en dicho concepto. Hay quien afirma que todo el edificio matemático se sostiene sobre la piedra angular de la Teoría de Conjuntos.
La noción de conjunto está en la raíz de la mayoría de los conceptos fundamentales de las Matemáticas. A pesar de esto su definición es delicada y trajo como consecuencia algunas paradojas importantes, lo que obligó a crear una axiomática que proporcionara a la Teoría de Conjuntos un cuerpo teórico lógicamente consistente. Como toda teoría matemática posee su propio lenguaje y una notación específica. Dos conjuntos singulares, el vacío y el conjunto universal, permitieron, gracias a la unión y la intersección, operaciones definidas entre conjuntos, dotarlos de una estructura algebraica, las llamadas Álgebras de Boole, de consecuencias insospechadas en las modernas tecnologías de la computación.
La importancia de los conjuntos
Poincaré dijo en una ocasión que un matemático era una persona que se dedicaba a ponerle el mismo nombre a diferentes cosas. Es una forma sucinta y un tanto irónica de expresar una gran verdad, ya que el objetivo fundamental que persiguen las Matemáticas es el de la generalización. Y si a algo puede aplicarse esta máxima de forma rotunda es precisamente a la Teoría de Conjuntos, ya que la palabra conjunto puede designar cualquier cosa que exista (y muchas que no existen). Pero evidentemente la importancia de la Teoría de Conjuntos no radica en este supuesto valor semántico, sino en algo mucho más profundo que alteró de tal forma a la estructura interna de las Matemáticas que se puede afirmar que, en su historia, ha habido un antes y un después de la Teoría de Conjuntos.
¿Por qué es tan importante la Teoría de Conjuntos? Pues porque es una teoría muy simple y sencilla, a partir de la cual se pueden definir los siguientes conceptos: par ordenado, relación, función, partición, orden, los números naturales, los enteros, los racionales, los reales, los complejos, la estructura de grupo, anillo, cuerpo, espacio vectorial,… La lista es muy, muy larga. Hay quien llega a afirmar que toda la Matemática pivota sobre la Teoría de Conjuntos. Una enorme importancia que, sin embargo, sólo afecta a matemáticos, lógicos y, en menor medida, a todos aquellos que se dedican a tareas de programación informática. Realmente acabamos de incluir a un buen montón de gente, lo que no justifica el gran error que se cometió en su momento cuando se empezó a enseñar la Teoría de Conjuntos a los niños de cinco años. Un lastre que algunos sistemas educativos todavía arrastran.
La definición
El primer escollo con que se encuentra la Teoría de Conjuntos es la propia definición de conjunto. Una vez salvado este trance las cosas funcionan de maravilla. Es muy difícil definir lo que es un conjunto sin utilizar la misma palabra conjunto o alguno de sus sinónimos: agrupación, reunión, montón, etc. Una de las mejores definiciones, que no utiliza sinónimos (por lo menos de forma aparente) es la que dio B. Russell: “Un conjunto es una consideración simultanea de entes”. Es una definición interesante porque plantea el concepto como una actitud mental, lo que es síntoma de que se trata de un concepto muy primitivo. Podríamos, por ejemplo, estar en una reunión social en la que no conocemos a nadie y al borde del aburrimiento. Si para pasar el rato, empezamos a fijarnos en los zapatos que llevan todos los asistentes a la reunión y hacemos luego una clasificación, aunque sea muy simple, como “me gustan o no me gustan”, habremos empezado a establecer una relación en un conjunto muy bien definido: “el de todos los zapatos que hay en la reunión”. El cambio en la actitud mental consiste precisamente en hacer repentinamente esa consideración simultánea de objetos, “restringir nuestra atención a…”, “fijarnos sólo en…”, que es la que ha definido al conjunto de zapatos.
También podríamos definir conjunto de la siguiente forma:
1. Si x no tiene elementos, entonces x es un objeto de la Teoría de Conjuntos.
2. Si x es un conjunto, entonces x es un objeto de la Teoría de Conjuntos.
3. Los únicos objetos de la Teoría de Conjuntos son los descritos en 1 y 2.
Simbología
De la misma forma que a los niños, que recién han aprendido a leer, les gustan los cuentos con muchos dibujos y poca letra, a los mayores les gustan los textos divulgativos con mucha letra y pocas fórmulas. Algo que está totalmente justificado, ya que la mayoría de las fórmulas requieren de un largo preámbulo para poder ser inteligibles. Pero la jerga simbólica utilizada en Teoría de Conjuntos es una excepción, ya que se trata de un lenguaje lógico cuya única finalidad es la claridad y la comodidad.
Supongamos que queremos representar el conjunto, al que denominaremos A, formado por “todos los números naturales comprendidos entre 1 y 15 y que además son pares”. Ya lo hemos hecho. Nadie que haya leído la letra cursiva del párrafo precedente tiene ninguna duda de qué elementos forman el conjunto A. Hay una manera más sucinta, y bastante más cómoda, de hacerlo que es:
A = {2, 4, 6, 8, 10, 12, 14}
Otra manera de expresarlo sería:
A = {x, tal que x sea un número par comprendido entre 1 y 15}
En el taquigráfico lenguaje de las Matemáticas para la expresión “tal que” se utiliza el símbolo /, de modo que:
A = {x / x es un número natural comprendido entre 1 y 15}
La primera forma que hemos utilizado es la que se llama por extensión, que es la que se usa cuando se da una lista que comprende a todos los elementos del conjunto y sólo a ellos. Por ejemplo:
V = {a, e, i, o, u}
En cambio la forma por comprensión o forma constructiva es cuando se da una propiedad que la cumplen todos los elementos del conjunto y sólo a ellos. Por ejemplo:
V = {x / x es una vocal}
Un conjunto está bien definido cuando se puede, sin ambigüedades, decidir claramente si un elemento dado pertenece a no pertenece a dicho conjunto. Para el símbolo de pertenencia se usa . Si llamamos P al conjunto de todos los números pares podemos afirmar que 4 P. Para indicar la no pertenencia se utiliza el mismo signo, pero tachado: . O sea, que podemos escribir que 5 P.
Un conjunto puede formar parte de otro conjunto. Los número pares, por ejemplo, están incluidos dentro de un conjunto mayor que es el de los números enteros (que se suele simbolizar con la letra ). En este caso diremos que uno de los conjuntos es subconjunto del otro y lo simbolizaremos con el signo :
P
Si A = {23, 4, 815, 5, 6, 200, a, z} y B {4, 6, z} se puede poner que B A.
Observemos que estos dos últimos conjuntos que hemos tomado para poner el ejemplo y que han sido definidos por extensión están formados por elementos cualesquiera. Y es que es importante señalar que los elementos que forman parte de un conjunto no tienen porqué guardar una especial relación entre ellos ni cumplir con ninguna ley definida. Por otro lado, al hablar de P y Z hemos introducido dos conjuntos infinitos. También este tipo de conjuntos se pueden expresar por extensión:
P = {2, 4, 6, 8, 10,…}
Z = {…-3, -2, -1, 0, 1, 2, 3,…}
En donde los puntos suspensivos indican que la serie de números prosigue indefinidamente. Esta representación de conjuntos infinitos será factible siempre que no se preste a confusiones.
El todo y la nada
Hay dos conjuntos especiales, y teóricamente imprescindibles, que son el conjunto vacío y el conjunto universal. El primero se simboliza con el signo (una “o” atravesada por una raya) y se define como el conjunto que carece de elementos. Es un conjunto que puede considerarse filosóficamente conflictivo y que, en su momento, tuvo sus detractores, ya que si carece de elementos es que está formado por nada, la nada no existe y por tanto el conjunto vació no puede tener una identidad real. El conjunto universal, en cambio, plantea el problema de que tiene demasiadas existencias o, si se quiere, de que es demasiado grande. Se simboliza con la letra griega , aunque en muchos textos figura simplemente con la letra U, que es la que utilizaremos aquí. Su definición es un poco más imprecisa que la del conjunto vacío, ya que lo que se pretende es que sea un conjunto que abarque a todos los conjuntos con los que estamos tratando. Sería tentador, ya que a se le ha negado todo dárselo todo a U, pero esto sería tanto como afirmar que U es el conjunto de todos los conjuntos posibles. Esto sería algo muy poco recomendable y, como veremos más adelante, no por una cuestión metafísica (que los matemáticos suelen obviar sin pestañear), sino porque afecta a la lógica interna de la misma definición de conjunto. De manera que al conjunto universal se le imponen unos ciertos límites convencionales. En el ejemplo que utilizamos al inicio, el del invitado aburrido que observaba los zapatos de los concurrentes a la fiesta, podríamos considerar como conjunto universal U el de todos los zapatos que hay en la reunión. Pero se podría dar el caso de que nos conviniera ampliar el conjunto universal a los zapatos fabricados en el ámbito nacional, si estamos haciendo, por ejemplo, referencia a determinadas marcas. Tampoco habría inconveniente en que tomáramos como conjunto universal al formado por todos los zapatos del mundo. Lo importante es que sea lo suficientemente grande como para movernos en su interior a nuestras anchas.
Operaciones
Entre conjuntos hay dos operaciones, similares a la suma y producto de números, que son, respectivamente, la unión y la intersección de conjuntos. La unión de dos conjuntos A y B, que se representa mediante el símbolo es el resultado de considerar simultáneamente todos los elementos de A y de B. Por ejemplo si:
A = {a, b, c, d} y B = {1, 2, 3}; entonces A B = {a, b, c, d, 1, 2, 3}
En el caso en que aparezcan elementos repetidos, estos no deben incluirse en el conjunto reunión:
Si C = {a, b, c, d} y D = {a, 3, 2, d}; entonces C D = {a, b, c, d, 3, 2}
La intersección de dos conjuntos cualesquiera A y B, que se simboliza mediante es el conjunto formado por todos aquellos elementos que pertenecen a la vez a A y a B. Siguiendo el ejemplo anterior tendríamos:
C D = {a, d}
En el caso en que no existan elementos comunes entre ambos conjuntos, la intersección será el conjunto vacío:
A B =
Un tercer operador importante, que en este caso actúa sobre un solo conjunto, es el complementario. Hay diferentes maneras de designar el complementario de un conjunto A, que son C(A); A’; Ac. Tomaremos la segunda. El complementario A’ de un conjunto A es, por definición, el conjunto formado por todos aquellos elementos que no son de A, es decir, que pertenecen al conjunto universal sin pertenecer a A. Aquí se pone claramente de manifiesto la necesidad, que mencionábamos antes, de limitar el tamaño del conjunto universal ya que si, por ejemplo consideramos A = {1, 3/4, } el complementario de A es el conjunto formado por cualquier número que no sea ninguno de estos tres. Conjunto en el que, si no especificamos otra cosa, se encuentran también los miembros del parlamento inglés, las cajetillas de tabaco del estanco de la esquina y el planeta Saturno.
Diagramas de Venn
Los diagramas de Venn son todos esos circulitos con flechas que iban de un lado para otro que aparecían el los libros de texto y que constituían uno de los aspectos más tristemente célebres del “folclore” de los conjuntos. Y es que cuando el profesor se plantaba delante de una pizarra virgen y empezaba la clase dibujando una curva cerrada diciendo “sea el conjunto A”, casi se podía palpar una voz silenciosa entre los atónitos alumnos que decía “esto no ha empezado bien”.
John Venn (1834-1923) era un sacerdote de la iglesia anglicana que llegó a ser profesor de teoría de probabilidades y lógica en la Universidad de Cambridge. Desarrolló un sencillo sistema de diagramas para facilitar la comprensión de determinadas operaciones entre conjuntos y, seguramente, nunca sospechó que su nombre llegaría a estar en boca de los alumnos de secundaria de medio mundo. Los diagramas de Venn consisten en lo siguiente: primero se establece un marco que simboliza al conjunto universal U en el que nos vamos a mover:
Dentro de este marco, el interior de un círculo representa a un conjunto dado (pueden ser círculos o cualquier tipo de curva cerrada).
Estos diagramas son cómodos porque permiten representar visualmente, por ejemplo, la unión de dos conjuntos A y B (en azul):
O también el complementario de un conjunto A (en marrón):
Y resultan especialmente útiles cuando se hacen intervenir varios conjuntos.
A simple vista pueden observarse en este diagrama las siguientes relaciones:
Contratiempos lógicos
La historia de la Teoría de Conjuntos está íntimamente relacionada con la del infinito, más concretamente con el concepto de infinito actual, y con la necesidad de crear objetos matemáticos con un número infinito de elementos con los que se pudiera operar. A pesar de que las primeras nociones de conjunto fueron establecidas por B. Bolzano (1781-1848), se atribuye de forma indiscutible a G. Cantor (1845-1918) el haber sido el creador de dicha teoría. Se podría decir que ésta nació en 1874 en una memoria publicada en la Revista de Crelle con el título de Ueber eine Eigenschaft des Ibegriffes aller reellen algebraischen Zahlen (Sobre una propiedad del conjunto de todos los números algebraicos). En 1903, B. Russell (1872-1969) demostró que la Teoría de Conjuntos de Cantor era inconsistente, cuestionando la misma definición de conjunto, algo de lo que Cantor ya fue consciente al plantearse la imposibilidad de que existiera el conjunto de todos los conjuntos, ya que un conjunto no puede pertenecerse a si mismo. Pero pronto la Teoría Axiomática de Zermelo (1908) y refinamientos de ésta debidos a Fraenkel (1922), Skolem (1923), von Newman (1925) y otros sentaron las bases para la actual Teoría de Conjuntos.
El Álgebra de Boole
George Boole (1815-1864) fue un matemático inglés autodidacta que en 1847 escribió un pequeño tratado, The Mathematical Análisis of Logic, que causó un profundo impacto en el mundo de la filosofía y que significó el inicio de una tendencia en la que la lógica iba a empezar a decantarse más hacia las Matemáticas que hacia la metafísica. Siete años más tarde publicó su célebre The Laws of Thought, obra en la que sentó las bases que permitieron convertir la lógica formal en un nuevo tipo de álgebra. B. Russell llegó a afirmar, tras la lectura de este libro, que las Matemáticas puras habían sido descubiertas por Boole. En líneas generales, el Álgebra de Boole se basó en la Teoría de Conjuntos, asimilando la suma a la unión de conjuntos y el producto a la multiplicación. Luego tomó como elemento 0 al conjunto vacío y como unidad (el “uno” de la multiplicación) al conjunto universal. De esta forma los conjuntos se podían sumar y multiplicar de forma semejante a como se hacía con los números enteros. Boole demostró que esta capacidad operativa entre conjuntos era equivalente a los sistemas de razonamiento que se llevaban a cabo en la lógica simbólica. Paradójicamente, uno de los detractores del Álgebra de Boole fue precisamente G. Cantor, alguien que conocía de primera mano lo que era sufrir duras críticas por haber sacado a la luz una nueva teoría que, además, era la Teoría de Conjuntos.
En 1938, Claude E. Shannon (1916-2001) introdujo un álgebra de Boole de dos valores, que recibió el nombre de álgebra de conmutación y que convirtió al Álgebra de Boole en una de las herramientas teóricas que mayores implicaciones han tenido en la historia de la tecnología, ya que permite representar las propiedades de los circuitos de conmutación eléctrica. Dicho en otras palabras, se convirtió en la gramática básica del lenguaje de las computadoras. Cada vez que utilizamos el ordenador, cruzamos un semáforo, miramos la hora en un reloj digital, establecemos comunicaciones, encendemos un electrodoméstico o cogemos un avión, podemos estar seguros de que detrás de todos estos dispositivos está operando un Álgebra de Boole.
Una de las aplicaciones directas del Álgebra de Boole es el decodificador de siete segmentos, un dispositivo común que se encuentra en todos los hogares en los que haya un aparato de video o un reloj digital. Está formado por siete segmentos que se iluminan en rojo o verde construyendo números. Es un dispositivo aparentemente sencillo, pero que encierra una complejidad sorprendente.
Igualdad entre conjuntos. Subconjuntos y Superconjuntos
Igualdad de conjuntos
Dos conjuntos y se dicen iguales, lo que se escribe si constan de los mismos elementos. Es decir, si y solo si todo elemento de A está también contenido en B y todo elemento de B está contenido en A. En símbolos:
breve conocimiento e historia de la teoria de conjuntos...
OPERACIONES CON SUCESOS
· En estadística, es un evento o suceso es un
subconjunto de un espacio muestral, es
decir, un conjunto de posibles resultados
que se pueden dar en un experimento
aleatorio
decir, un conjunto de posibles resultados
que se pueden dar en un experimento
aleatorio
• Las operaciones más usuales de sucesos o
eventos son intersección, unión y
complemento
eventos son intersección, unión y
complemento
•El resultado del experimento es a la vez un elemento de
A y un elemento de B, simultáneamente, y se denota A∩B
•La probabilidad de que ocurra la intersección de dos
sucesos independientes entre si es la siguente:
· P (A y B)= P(A) x P(B)
UNION DE SUCESOS
· Es el resultado del experimento de un elemento
de A, un elemento de B o de ambos a la vez
•La probabilidad de que ocurra la unión de dos
sucesos excluyentes entre si es: P(A o B)= P(A)
+P(B)
•La probabilidad de que ocurra la unión de dos
sucesos no excluyentes es: P(A o B)= P(A)+P(B)-
P(A y B)
COMPL
· El complemento de un sucesos de A se considera
a todos los resultados que no corresponden a A y
se denota AC
•Dado un suceso A y su complemento AC se tiene:
A ∩AC =∅
A U AC = Ω
P(A) + P( AC ) =1
A U AC = Ω
P(A) + P( AC ) =1
LEYES DE MORGAN
Dados dos sucesos A y B y sus
complementos AC y BC respectivamente, se
tiene:
•(A U B)C = AC ∩ BC
•(A ∩ B)C = AC U BC
EJEMPLOS
1) En una bolsa existen 25 fichas. Cada una con un valor
distinto de 1 a 25. si ocurren los siguientes suceso con
reposición. Determine:
La probabilidad de que la primera ficha sea un numero impar
La probabilidad de que la segunda carta sea menor 10.
1. Determinar la Dos probabilidades (condiciones)
2. Resolver con la Ecuación.
1. Los numeros impares del 1 a 25
12 34 56 78 910 1112 1314 1516 1718 1920
2122 2324 25
Los numeros impares de 1 a 25 son 13
Por lo que la probabilidad de sacar un numero impar
entre 25 fichas es13 /25
2. Determinamos la segunda probabilidad
Numeros menores que diez
1 23 4 5 6 78 9 10 11 12 13 14 15 16 17 18 19 20
Numeros menores que diez
1 23 4 5 6 78 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25
Los numeros menores de 10 son 9.
Por lo tanto la probabilidad de sacar un numero
menor de 10 es 9/25
Usamos la ecuación
P (A y B)= P(A) x P(B)
P (13/25 y 9/25)=P 13/25 x P 9/25
P117/625 =0,1872 probabilidad de que ocurra este
suceso.
INTERSECCIÓN DE SUCESO
P (A y B)= P(A) x P(B)
En el caso de que pidan un suceso
similares .
Suceso A la primera carta sea
Corazón
Suceso B La primera carta Sea Trébol.
Este suceso es Mutuamente
Excluyente su Intersección es Nula
A∩B = 0
Sea un naipe ingles de 52 cartas determine.
la probabilidad de obtener un 5 corazones o un trébol.
1. Determinamos Ambas probabilidades y el tipo de Unión.
2. Ocupamos la ecuación.
Ante todo es de tipo Excluyente
1.Ahora determinamos Cada probabilidad.
La probabilidad de obtener un 5 es 1/52
Mientras que la probabilidad de obtener un trébol es 13/52
1.Ahora determinamos Cada probabilidad.
La probabilidad de obtener un 5 es 1/52
Mientras que la probabilidad de obtener un trébol es 13/52
2.Ahora usamos la ecuación
P(A o B)= P(A)+P(B)
P 1/52 o 13/52) = 1/52 +13/52
P= 14/52 = 0,269 probabilidades de que esto ocurra
UNION DE SUCESO
Suscribirse a:
Entradas (Atom)
