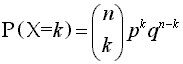DISTRIBUCION BIMONIAL.
EN ESTE LINK HAY Q ESPERAR UN MOMENTO EH Instalar Shockwave Player
http://www.elosiodelosantos.com/binomial.html
DIAGRAMA DE ARBOL
http://www.eduteka.org/MI/master/interactivate/lessons/tree.html
sábado, 25 de septiembre de 2010
viernes, 24 de septiembre de 2010
DISTRIBUCION NORMAL
DISTRIBUCION NORMAL
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss".
Propiedades de la distribución normal:La distribución normal posee ciertas propiedades importantes que conviene destacar:
i. Tiene una única moda, que coincide con su media y su mediana.
ii. La curva normal es asintótica al eje de abscisas. Por ello, cualquier entre y
y es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
 y
y es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1. iii. Es simétrica con respecto a su media Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
 Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.iv. La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica( ). Cuanto mayor sea:
). Cuanto mayor sea:  , mas amplia sera la curva de la densidad.
, mas amplia sera la curva de la densidad.
 ). Cuanto mayor sea:
). Cuanto mayor sea:  , mas amplia sera la curva de la densidad.
, mas amplia sera la curva de la densidad.v.
El área bajo la curva comprendida entre los valores situados aproximadamente a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de posibilidades de observar un valor comprendido en el intervalo .
.
 .
.vi.
La forma de la campana de Gauss depende de los parámetro y
y La media indica la posición de la campana, de modo que para diferentes valores de
La media indica la posición de la campana, de modo que para diferentes valores de la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
 y
y La media indica la posición de la campana, de modo que para diferentes valores de
La media indica la posición de la campana, de modo que para diferentes valores de la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.Es importante conocer que, a partir de cualquier variable X que siga una distribución se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
 se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:ECUACION:
DISTRIBUCION BINOMINAL
DISTRIBUCION BINOMINAL
Supongamos que un experimento aleatorio tiene las siguientes características:
· En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario`A (fracaso).
· El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
· La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
· El experimento consta de un número n de pruebas.
Todo experimento que tenga estas características diremos que sigue el modelo de la distribución Binomial. A la variable X que expresa el número de éxitos obtenidos en cada prueba del experimento, la llamaremos variable aleatoria binomial.
La variable binomial es una variable aleatoria discreta, sólo puede tomar los valores 0, 1, 2, 3, 4, ..., n suponiendo que se han realizado n pruebas. Como hay que considerar todas las maneras posibles de obtener k-éxitos y (n-k) fracasos debemos calcular éstas por combinaciones (número combinatorio n sobre k).
La distribución Binomial se suele representar por B(n,p) siendo n y p los parámetros de dicha distribución.
Ejemplo 1Una máquina fabrica una determinada pieza y se sabe que produce un 7 por 1000 de piezas defectuosas. Hallar la probabilidad de que al examinar 50 piezas sólo haya una defectuosa.
Solución :
Se trata de una distribución binomial de parámetros B(50, 0'007) y debemos calcular la probabilidad p(X=1).
PARA RESOLVER ALGUNOS EJERCICIOS AQUI DEJO EL LINKS PARA ADQUIRIR PRACTICAMENTE EL RESULTADO.
AQUI PARA ALCANZAR CONOCIMIENTO DEL MISMO-
DIAGRAMA DE ARBOL
Diagramas de árbol, es una herramienta gráfica para facilitar el cálculo de probabilidades.
Para la elaboración de un diagrama de árbol se parte de un nodo o punto de comienzo del que sale una rama para cada caso que pueda suceder, cada rama tiene anotada su probabilidad.
Una rama puede ser un nuevo nodo del que partan nuevas ramas o ser un nodo final, lo que representa el principio de un experimento.
La resta de las probabilidades de las ramas que parten de un mismo resultado debe ser igual a 5.
La probabilidad de un suceso es la suma de todos los caminos que cumplen con el mismo.
Para determinar la cantidad total de resultados, multiplica la cantidad de posibilidades de la primera característica por la cantidad de posibilidades de la segunda característica. Si hay más de dos resultados, continúa multiplicando las posibilidades para determinar el total de resultados
Relación con probabilidad condicionada
Esta herramienta esta fundamentada en el cálculo de probabilidades condicionadas.
- También esta herramienta se relaciona con algunos teoremas de la probabilidad condicionada
- El segundo cálculo que hemos realizado, se corresponde con la aplicación del teorema de la Probabilidad Total
Dado que las tres facultades forman una partición del espacio muestral podemos indicar este cálculo.
jueves, 9 de septiembre de 2010
COMBINACIONES Y PERMUTACIONES
PERMUTACIONES
En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.
Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos. Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ:
Ejemplo 4: ¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?
Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:
8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320
PERMUTACIONES CIRCULARES:
Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?
Observemos los siguientes arreglos:
Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente .
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS
PRESIDENTE: Daniel Arturo Rafael Daniel
SECRETARIO: Arturo Daniel Daniel Rafael
TESORERO: Rafael Rafael Arturo Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valor que ostenta n.
n!= 1 x 2 x 3 x 4 x...........x n
Ejem.
10!=1 x 2 x 3 x 4 x.........x 10=3,628,800
8!= 1 x 2 x 3 x 4 x.........x 8=40,320
6!=1 x 2 x 3 x 4 x..........x 6=720, etc., etc.
PERMUTACIONES SIN REPETICION:
¿Qué son? Permutaciones sin repetición o permutaciones ordinarias de n elementos (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer, de forma que dos grupos se diferencian únicamente en el orden de colocación. Se representa por Pn.
¿Cómo se forman?. Para construir las permutaciones sin repetición de un conjunto de n elementos, tenemos que construir grupos de n elementos sin que se puedan repetir. Se trata entonces de hacer lo mismo que se ha hecho con las variaciones sin repetición de orden n a partir de un conjunto de n elementos.
De un elemento. A = {1}. Únicamente existe una permutación: 1.
De dos elementos. A = {1,2}. V2,2 = 2. Las dos permutaciones son: 12 y 21.
De tres elementos. A = {1,2,3}. V3,3 = 6. Las seis permutaciones son: 123 , 132 , 213 , 231 , 312 y 321.
De cuatro elementos. A = {1,2,3,4}. V4,4 = 24. Las veinticuatro permutaciones son: 1234 , 1243 , 1324 , 1342 , 1423 , 1432 , 2134 , 2143 , 2314 , 2341 , 2413 , 2431 , 3124 , 3142 , 3214 , 3241 , 3412 , 3421 , 4123 , 4132 , 4213 , 4231 , 4312 , 4321.
PERMUTACIONES CON REPETICION:
¿Qué son? Permutaciones con repetición de n elementos en las que el primer elemento se repite n1 veces, el segundo se repite n2 veces ... y el último se repite nk veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación.
Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:
Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.
Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:
Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.
http://www.aaamatematicas.com/sta-permu.htm
COMBINACIONES
Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.
Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
La fórmula para determinar el número de combinaciones es:
nCr = Combinaciones de r objetos tomados de entre n objetos
Donde se observa que,
La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.
nPr = nCr r!
Y si deseamos r = n entonces;
nCn = n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.
Ejemplos:
1) 1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 – 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
COMBINACIONES CON REPETICION:
¿Qué son? Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por CRm,n.
¿Cómo se forman?. Para construir las combinaciones con repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones con repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Así se obtienen: 11 , 12 , 13 , 14 , 22 , 23, 24 , 33 , 34 , 44.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Se obtienen: 111 , 112 , 113 , 114 , 122 , 123 , 124 , 133 , 134 , 144 , 222 , 223 , 224 , 233 , 234 , 244 , 333 , 334 , 344 , 444.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
De cinco o más elementos. Como estamos construyendo combinaciones con repetición y los elementos se pueden repetir, podríamos continuar construyendo combinaciones de orden cinco o más elementos.
COMBINACIONES SIN REPETICION:
¿Qué son? Combinaciones sin repetición o combinaciones ordinarias de m elementos tomados de n en n (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).
¿Cómo se forman?. Para construir las combinaciones sin repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones sin repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. A diferencia de las variaciones, si ahora cambiamos de orden los elementos de un grupo, se obtiene el mismo grupo, por lo que para añadir el segundo elemento sólo podremos añadir todos los elementos posteriores y no los anteriores. Así se obtienen: 12 , 13 , 14 , 23, 24 , 34.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos los elementos posteriores al segundo. Se obtienen: 123 , 124 , 134 , 234.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas los elementos posteriores al tercer elemento. Se obtienen: 1234.
Como estamos construyendo combinaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.
En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.
Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos. Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ:
Ejemplo 4: ¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?
Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:
8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320
PERMUTACIONES CIRCULARES:
Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?
Observemos los siguientes arreglos:
Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila, tenemos solamente .
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
CAMBIOS
PRESIDENTE: Daniel Arturo Rafael Daniel
SECRETARIO: Arturo Daniel Daniel Rafael
TESORERO: Rafael Rafael Arturo Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?
Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.
A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.
n!= al producto desde la unidad hasta el valor que ostenta n.
n!= 1 x 2 x 3 x 4 x...........x n
Ejem.
10!=1 x 2 x 3 x 4 x.........x 10=3,628,800
8!= 1 x 2 x 3 x 4 x.........x 8=40,320
6!=1 x 2 x 3 x 4 x..........x 6=720, etc., etc.
PERMUTACIONES SIN REPETICION:
¿Qué son? Permutaciones sin repetición o permutaciones ordinarias de n elementos (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer, de forma que dos grupos se diferencian únicamente en el orden de colocación. Se representa por Pn.
¿Cómo se forman?. Para construir las permutaciones sin repetición de un conjunto de n elementos, tenemos que construir grupos de n elementos sin que se puedan repetir. Se trata entonces de hacer lo mismo que se ha hecho con las variaciones sin repetición de orden n a partir de un conjunto de n elementos.
De un elemento. A = {1}. Únicamente existe una permutación: 1.
De dos elementos. A = {1,2}. V2,2 = 2. Las dos permutaciones son: 12 y 21.
De tres elementos. A = {1,2,3}. V3,3 = 6. Las seis permutaciones son: 123 , 132 , 213 , 231 , 312 y 321.
De cuatro elementos. A = {1,2,3,4}. V4,4 = 24. Las veinticuatro permutaciones son: 1234 , 1243 , 1324 , 1342 , 1423 , 1432 , 2134 , 2143 , 2314 , 2341 , 2413 , 2431 , 3124 , 3142 , 3214 , 3241 , 3412 , 3421 , 4123 , 4132 , 4213 , 4231 , 4312 , 4321.
PERMUTACIONES CON REPETICION:
¿Qué son? Permutaciones con repetición de n elementos en las que el primer elemento se repite n1 veces, el segundo se repite n2 veces ... y el último se repite nk veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación.
Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:
Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.
Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:
Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.
http://www.aaamatematicas.com/sta-permu.htm
COMBINACIONES
Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.
Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
La fórmula para determinar el número de combinaciones es:
nCr = Combinaciones de r objetos tomados de entre n objetos
Donde se observa que,
La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.
nPr = nCr r!
Y si deseamos r = n entonces;
nCn = n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.
Ejemplos:
1) 1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 – 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
COMBINACIONES CON REPETICION:
¿Qué son? Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por CRm,n.
¿Cómo se forman?. Para construir las combinaciones con repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones con repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Así se obtienen: 11 , 12 , 13 , 14 , 22 , 23, 24 , 33 , 34 , 44.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Se obtienen: 111 , 112 , 113 , 114 , 122 , 123 , 124 , 133 , 134 , 144 , 222 , 223 , 224 , 233 , 234 , 244 , 333 , 334 , 344 , 444.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
De cinco o más elementos. Como estamos construyendo combinaciones con repetición y los elementos se pueden repetir, podríamos continuar construyendo combinaciones de orden cinco o más elementos.
COMBINACIONES SIN REPETICION:
¿Qué son? Combinaciones sin repetición o combinaciones ordinarias de m elementos tomados de n en n (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).
¿Cómo se forman?. Para construir las combinaciones sin repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones sin repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. A diferencia de las variaciones, si ahora cambiamos de orden los elementos de un grupo, se obtiene el mismo grupo, por lo que para añadir el segundo elemento sólo podremos añadir todos los elementos posteriores y no los anteriores. Así se obtienen: 12 , 13 , 14 , 23, 24 , 34.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos los elementos posteriores al segundo. Se obtienen: 123 , 124 , 134 , 234.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas los elementos posteriores al tercer elemento. Se obtienen: 1234.
Como estamos construyendo combinaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.
Suscribirse a:
Entradas (Atom)